Odd and Even Investigations
eg) Ages of people in your family.
Phone number
Street number
Height etc..
Investigating: Odd and Even....Add some combinations of the facts you found.
odd + odd = ?
odd + odd + odd = ?
etc..
even + even = ?
odd + even = ?
Can you find any patterns and generalisations? How is this useful?
Having fun with Capacity and Mass
Students are encouraged to use their own strategies to solve problems: Here are a few ideas:
Some Multiplication strategies:
LATTICE MULTIPLICATION
eg) Ages of people in your family.
Phone number
Street number
Height etc..
Investigating: Odd and Even....Add some combinations of the facts you found.
odd + odd = ?
odd + odd + odd = ?
etc..
even + even = ?
odd + even = ?
Can you find any patterns and generalisations? How is this useful?
Having fun with Capacity and Mass
Students are encouraged to use their own strategies to solve problems: Here are a few ideas:
Some Multiplication strategies:
Grid Multiplication
Traditional Multiplication Algorithms
Investigation with 'Hundreds and Thousands'
(Sprinkles cake toppings).
I've always wondered how many 'Hundreds and Thousands' there are in a jar. Here's an investigation to help with Estimation, Place Value, Rounding, Area, Capacity, Multiplicative Thinking, Addition and many other things!
Division - Hands On Investigations
Ellen substituted the remainders for pieces of paper which she could then divide up into 6 pieces each. She then added the total of the whole amounts as well as the fraction that each would get and recorded the total as 3 and 2/6 each.
Roman Numerals
For more help with Roman Numerals, go to:
PLACE VALUE:
FLUENCY OF OPERATIONS:
INCREASE YOUR MATHS FLUENCY - CHECK THE 'WEBSITE LINKS' TAB ON THE TOP OF THIS BLOG, OR TRY THIS SITE: CLICK ON THIS LINK...
ARCADEMIC SKILL BUILDERS
Fun arcade style games to increase skills and fluency
NUMBER PATTERNS AND SEQUENCES GAME: CLICK ON THIS LINK TO TAKE YOU TO THE BBC.CO.UK SITE WITH EXCELLENT ACTIVITIES...
HTTP://WWW.BBC.CO.UK/BITESIZE/KS2/MATHS/NUMBER/NUMBER_PATTERNS/PLAY/
Money Worded Problems
Problem Solving Fun
Measuring angles areas and perimeters.
Measuring length and perimeter using string for curved parts. Measuring area using newspaper 1m x 2m. Then finding things around the school that had a similar area.
Task: Draw around the body. Measure the height of the person. Measure how many of their footsteps will fit into the height. (Most people found it was about 6 - 7 footsteps) Then add clothing by tracing shape blocks. Measure area and perimeter of various features.
Investigating volume, capacity and Mass.
Draw, make and measure volume. Count blocks.
Try formula l x w x h. Do you get the same result?
Capacity: Students used 30 mL cups to estimate how much rice would fit into 3 other containers.
Volume: Students measured the water displacement caused by a 1 cubic cm block. They noticed it moved the water level 1 mL. Then they tried to find the volume of other irregular objects by measuring the water displacement. 1mL water is displaced by 1 cm3
i.e.) 250mL displaced water = volume of 250cm3
i.e.) 250mL displaced water = volume of 250cm3
Students used a variety of scales to compare the mass of different objects. They had to estimate, compare and work out the difference. We discussed the difference between weight and mass. Mass is a measure of how much matter an object has. Weight is a measure of how strongly gravity pulls on that matter. On the moon, your weight would change because gravity is weaker but your mass would stay the same because you are still made up of the same amount of matter. Weight can be measured with spring scales.
Metric Conversion. Use this to help:
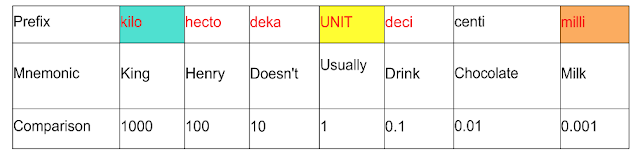
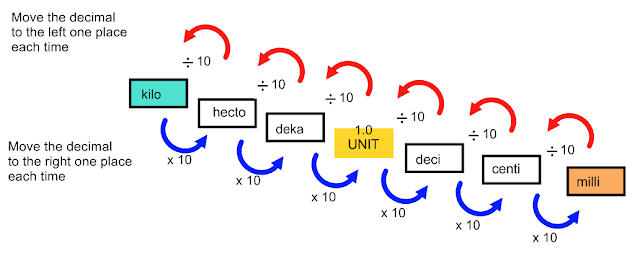
Children need to realise that if there is no decimal place in a number they can put one at the end e.g.) 3 = 3.0
Then they can convert to other units by moving the decimal place.
5 cm = 50 mm
5 cm = 0.05 m
5 cm = 0.00005km
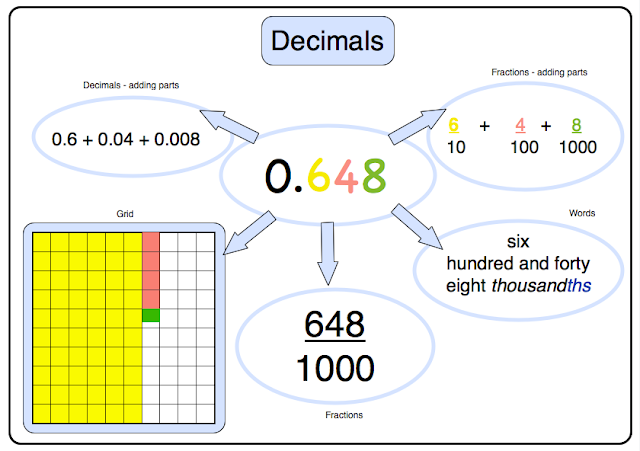
Using Decimals
There are a number of ways to express decimals: See if can find more ways to add to this: (For example, 64 hundredths + 8 thousandths.)
Always Estimate!
Estimate: See if you are close to the place value you get in the answer.
Example 1) 5432 x 25 is close to 5000 x 30 = 150,000
Example 2) 3572 x 67 is close to 4000 x 70 = 280,000
Example 1) 5432 x 25 is close to 5000 x 30 = 150,000
Example 2) 3572 x 67 is close to 4000 x 70 = 280,000
Terms to Revise:
Factors: 2 x 3 = 6 Factors are numbers you can multiply together to get another number.
Multiple: A number can be added to itself many times: Multiples of 5 are: 5,10,15,20, 25 30 etc...
Prime: A number that can only be divided by itself and 1 (It only has 2 factors)
e.g. 2,3,5,7,11,13,17,19 etc
Composite= More that 2 factors. e.g The number 24 is composite: It has (1,24) (2,12) (3,8) and (4,6) as factors.
Square = A number multiplied by itself will give a square number. e.g.) 3x3 = 9 (9 is a square number) 4x4=16, 5x5 = 25
Or...Check out this MATHS dictionary link http://www.amathsdictionaryforkids.com/dictionary.html
Or...Check out this MATHS dictionary link http://www.amathsdictionaryforkids.com/dictionary.html
Using factors to help with multiplying larger numbers.
Did you know if you find the PRIME factors of a number, you can also work out the answer?
eg) Look at 24 x 32
More ideas:
WORDED PROBLEM SOLVING
These are some worded problems you can try. They may help with preparation for NAPLAN.
The answers are below if needed!
Page 1
- Problem Solving can be challenging to many children - This site is great for practicing different strategies:

'Hands On' Maths....Make an easy Child's Abacus
TIMES TABLES STRATEGIES
Who wants to cut down on the number of tables they need to learn?
Colour in all the tables you already know on a grid: You probably know these:
Anything x 0 = 0
A number x 1 = the same number
A number x 10 = the number with a 0 on the end.
5 x pattern (0,5,0,5,0..)
If you can double numbers to 20, colour all the 2x tables
Look how many you already know!!
NOW....
Did you know you can swap the factors around? e.g.) 2 x 5 is the same result as 5 x 2 - This is called the "Commutative" property. Look at the tables you have already coloured. Now colour in all the facts that can be swapped around. (You may see a pattern!)
If you do all of the above numbers, you only end up having to learn 21 facts!
TRY learning the "Square" facts - These can help you work out others too. 3x3, 4x4, 5x5 etc.
(If you draw these in dot groups (arrays) they form a 'square')
Another important skill is to learn how to double (and halve) numbers.
If you know your 2x tables, then you just double these to get your 4x tables.
eg) 7 x4 is the same as 7 x2 x2 (4=2x2)
8x4 is the same as 8 x 2 x 2 etc...
If you double it again, you can do your 8 times tables
eg) 7 x8 is the same as 7 x2 x2 x2 (8=2x2x2)
9x8 is the same as 9 x 2 x 2 x 2 etc...
In other words, if you want to work out 6 x 8, you can work out 6 x 2 = 12, then double it twice
6x2 = 12, 12x2 = 24, 24x2 = 48.... SO 6 x 8 = 48
A similar principle applies to the 3, 6 and 12 times tables. (double 3 is 6, double again is 12) So....
If you want to work out 8 x 12, you can work out 8 x 3 and double it twice.
8 x 3 = 24, 24 x 2 = 48, 48 x 2 = 96.... SO 8 x 12 = 96
There are so many patterns and tricks that can help you.
Chanting or singing the tables is one way, but if is more helpful if you understand the patterns in case you forget the song. Happy memorising!
Who wants to cut down on the number of tables they need to learn?
In other words, if you want to work out 6 x 8, you can work out 6 x 2 = 12, then double it twice
6x2 = 12, 12x2 = 24, 24x2 = 48.... SO 6 x 8 = 48
A similar principle applies to the 3, 6 and 12 times tables. (double 3 is 6, double again is 12) So....
If you want to work out 8 x 12, you can work out 8 x 3 and double it twice.
8 x 3 = 24, 24 x 2 = 48, 48 x 2 = 96.... SO 8 x 12 = 96
There are so many patterns and tricks that can help you.
Chanting or singing the tables is one way, but if is more helpful if you understand the patterns in case you forget the song. Happy memorising!
CHECK OUT THIS WEBSITE FOR MORE HELP WITH TABLES STRATEGIES:
Try this easy way to learn your table multiples!
How to make a string tables multiples helper!
Watch the video above, then follow these instructions:- If you go clockwise you get multiples of 2. If you go the opposite way you get multiples of 8.
- If you do the multiples of 3 clockwise, you will get the multiples of 7 anticlockwise.
- If you do the multiples of 4 clockwise, you will get the multiples of 6 anticlockwise...etc
- Notice that the 2 numbers equal 10 each time... (2, 8) (3, 7) etc....
The finished product.
How to do it....
See how it can be used here:
More ideas:
Here are some Triangle facts for helping you with your 3 x and 6 x tables!
This chart points out the relationships between your 3 times and 6 times tables. If you know your 3x tables, you can work out your 6x tables by doubling.
There are many relationships that you can see using these triangles. e.g.) The black numbers represent the 3x tables in the triangles. (The red numbers are the 6x tables) Here are some facts from the 3x tables...
3x4=12 12÷4=3
4x3=12 12÷3=4
1/3 of 12 = 4
1/4 of 12 = 3
To see the relationship of 3's to 6's:
4x3=12
4x6=24
5x3=15
5x6=30
Notice how you can double them - because 6 is double 3!
Have a look at this! A great website for showing the patterns between 3, 6 and 9 using a Tic Tac Toe grid!
Follow this link: 3,6 and 9 times tables patterns!
Fluency Drills - 4 Operations and Strategies
This is a sample of some Fluency Drills and the strategies we discuss after completing them.
2012
Australian Mathematics Competition: Certificates for Credits and Distinctions were presented at assembly. 71% of our students received Proficiency or above. Well done!
Other Maths Competitions: Maths Mastermind. I put a competition in the fortnightly newsletter. Anyone can enter. Winners are announced at each assembly.
Whole school lunchtime Maths activities this year:
- We have had a Maths Graffiti Wall, where students recorded things they knew about Maths.
- We had a "Grand Designs" competition where students made large 3D structures out of rolled up newspaper.
- We had a "Great Race" where students had to race around the school to find objects and describe their location.
It is important to use ESTIMATING skills and practice problems based in a real life context.
Learning to estimate your result first is important.
Then you know if your result is reasonable or not.
To estimate, it is useful to round numbers.
This saying may help:
- Find the number, look next door
- 4 or less, just ignore
- 5 or more, add one more
- Chop off the heads of the ones that follow
Here is an example:
365
- Find the number (3) ............look next door..... (6)
- 4 or less, just ignore (The number next door.... (6)..... is more than 4.. so this part of the saying doesn't apply)
- 5 or more, add one more. (So we add one more to our original number ...3 becomes 4)
- 'Chop off the heads' of the ones that follow (add 0's)
So...the rounded number is.......400
In other words, if the number next door is 5 or higher, add one more to the original number
If the number is 4 or less, leave the original number as it is.
Then make all the others into 0's.
Addition Worded Problems....Try these, estimating first:
Lots of children get confused when subtracting with lots of zeros. This is just another strategy....
Did you know that you can subtract one at the start and then add it at the end?
eg) Work out: 4000 - 236
3999 (Subtract 1 from 4000)
- 236
______
3763 Now ADD 1 to this result.
______
= 3764
Addition and Subtraction Worded Problems
Fractions Worded Problems
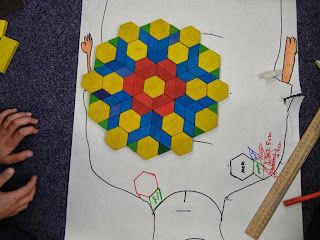
Fun with shapes. Children experimented with pattern blocks to create designs. They investigated tessellations.
.jpg)
.jpg)
Fun with Tangrams
Learning about area
Data and Graphing
Making Pictographs on Excel
























.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)




















.jpg)

.JPG)



.jpg)




































.jpg)
.jpg)
.jpg)
.jpg)
.jpg)

.jpg)





Have a look at the Favourite Apps page, for more help with learning your tables!
ReplyDeleteIf you want to participate in the Maths Mastermind competition at school, read the newsletter questions, and put your answers in the box in the front office. Winners will be given a certificate and prize. GOOD LUCK!
ReplyDelete